Calculating the distance to the Moon

On 13th sept 2019, Pauline Acalin, a spaceflight photojournalist, posted two pictures of the Moon, taken 8.5 hours apart. Scott Manley commented “I should try measuring the distance to the Moon with this”.

That’s was more than enough to get me started to attempt to do exactly this. After months of procrastination, here is finally an article with my findings and the detailed steps to reproduce them.

Two-frames GIF showing the Moon, 8.5 hours apart. A small difference can be seen: a rotation in the horizontal axis.
“Rotating planets come in handy when you want to make a giant stereoscopic gif of the moon […]” - Pauline Acalin

Introduction

The size of the Earth will be assumed to be known. In fact, it is since a long time. With this information and with the two pictures of the Moon, we are going to measure the distance to the Moon.

Let’s start with schema with the various known and unknown lengths, to get a better overview. If high school is not too far, you should quickly remember which equation can be used.

The Earth and the Moon aligned on two triangles, allowing the use of Thales' Theorem
Thales' Theorem anyone?

We will approximate a lot of things in order to be able to find an equation. On this schema, dist_earth_moon is not really the distance between the Earth and the Moon. But it should be close enough. The radiuses are small enough to be negligible. In any case, once this approximated value is computed, we can always come back and make our equation more precise.

The following equation can be stated: Earth_diff/Moon_diff = (dist_earth_moon+Moon_radius)/Moon_radius. It can be assumed that Moon_radius is very small compared to dist_earth_moon, which means that dist_earth_moon+Moon_radius ~= dist_earth_moon. Therefore, the equation become: Earth_diff/Moon_diff = dist_earth_moon/Moon_radius.

In this equation, Earth_diff can be computed (with the Earth’s radius and 8.5h), Moon_diff as well (we have two pictures to compute the displacement of a given point) and we want to compute dist_earth_moon. That leaves us with one unknown: Moon_radius. The trick is that Earth_diff and dist_earth_moon are going to be expressed in km, but Moon_diff and Moon_radius can not: the pictures do not give this information. Instead, they can be expressed in pixels, which will cancel out, leaving us with only km for dist_earth_moon.

Reorganizing the equation, it leads us to: dist_earth_moon_km = Earth_diff_km*Moon_radius_pxl/Moon_diff_pxl.

Part I - counting hours and pixels

Converting hours to km: earth_diff_km

Calculating the distance between the two pictures is simple trigonometry.

First of all, 8.5 hours is 8.5/24 * 2*pi = 2.23 radians. Then, for the distance, we can use several equations. One is E_diff = E_radius * 2*sin(2.22/2).

The Earth with two points on its surface, 8.5 hours apart.
This one should be easy

With an approximate value of 14 000 km given by Eratosthenes for the diameter of Earth, we find Earth_diff = 14000/2 * 2*sin(8.5/24 * 2*pi / 2) = 12 550 km.

Pretty easy.

Counting pixels: moon_radius_pxl and moon_diff_pxl

Counting Moon_radius_pxl is easy: we can find that the Moon appears to be 974 pixels wide.

But computing Moon_diff_pxl requires a bit more thinking. We want to find the difference between the two images, which corresponds to basically measuring (in pixels) the shift of a given specific point on the Moon between the two pictures.

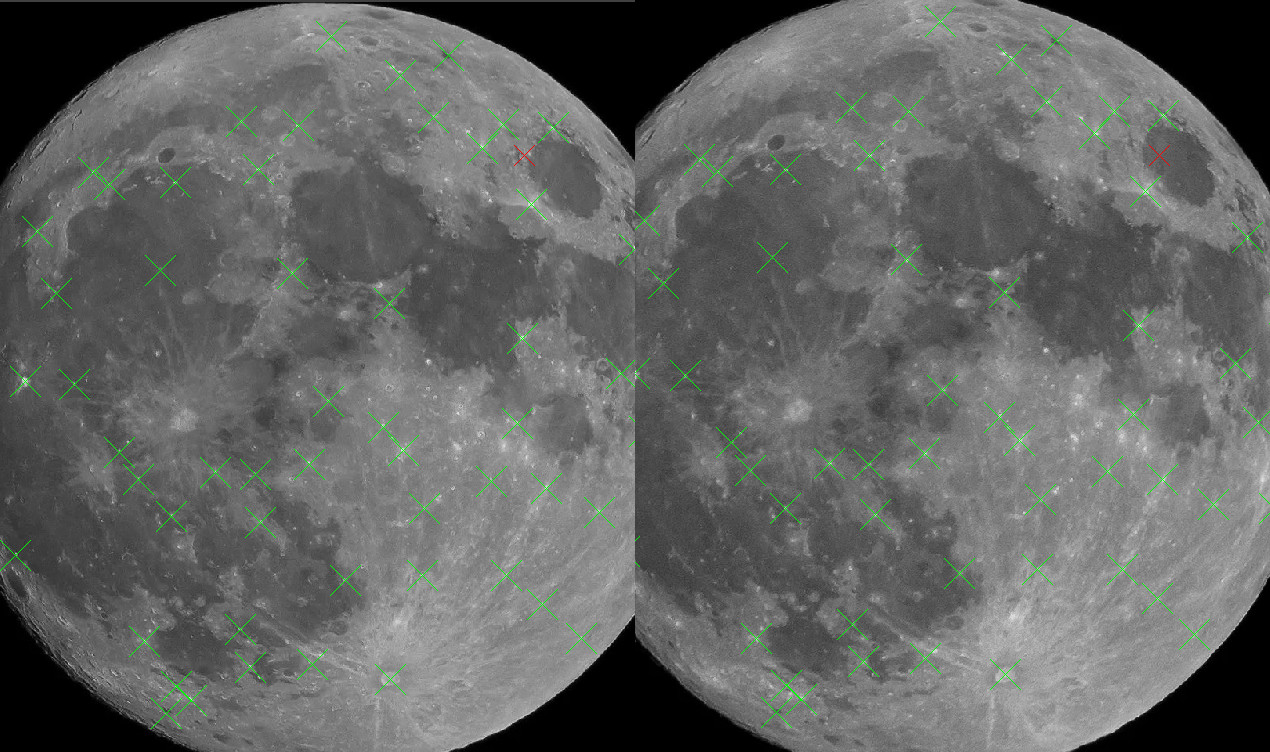
First of all, in order to have meaningful coordinates, I cropped the two images. The final size was the same: 974x987, which make both images aligned, and do not require further modifications to align their coordinates.

I had already a small piece of code, point marker, to mark specific points on two images and print their coordinates (it was used for an old project about reverse engineering the trajectory of a RocketLab rocket). This program allows one to see two images, and mark matching points on both. The coordinates of the points are then exported and can be use to compute a map of the displacement of the image between the two pictures.

I marked 57 points, more or less equally distributed on the whole surface of the Moon.

Two images of the Moon side by side, with dozens of crosses at the same place on each.
It is faster to do that you would expect

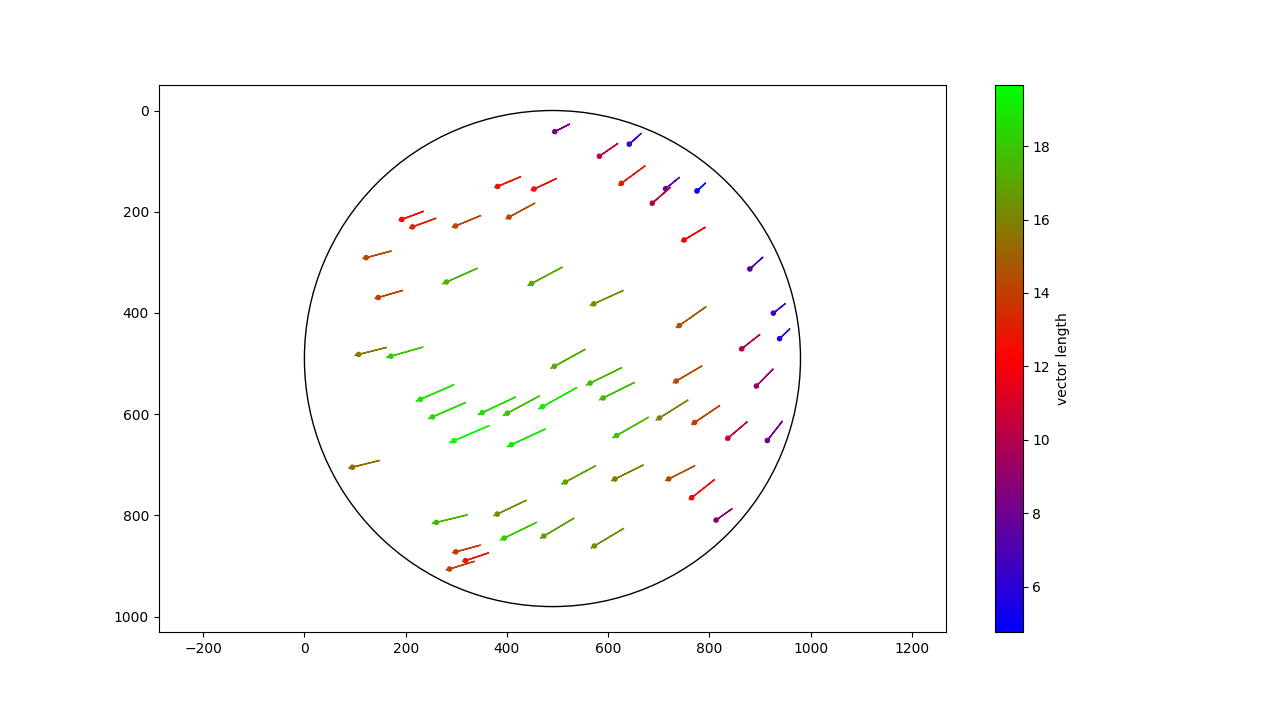
With the coordinates of the points I was able to compute displacement vectors as shown on the following graph.

A circle (the Moon) with dozens of vectors of various size (roughly 5 to 20). They are mostly horizontal, with the largest one around the center.
Ideally we would have more vectors, but this looks good enough

The displacement was of course very variable, depending on the position on the surface of the Moon: on the center close to the equator it moves more than close to the poles or on the sides.

I found vector length to be between 4.8 and 19.7 pixels. The average or mean are probably not very relevant here, as it depends on the location of the (manually chosen) points. The final value should probably be the largest, hence 19.7 pixels.

Wait.

When doing physics computations, one should always do a quick sanity check by verifying the units and the direction of the vectors.

Have we done that?

Let’s check the direction of the vectors: since the second picture was taken from a location more on the left compared to the first, we should expect a given point on the Moon to move to the right… But that’s not the case, all the vectors points to the left. Houston, we have a problem.

Part II - second attempt

Moon orbit and rotation

We assumed that the Moon is always showing us the same face, and that the Moon rotation did not have any influence in our calculations.

The first part is true: the Moon is tidally locked. It means that the Moon achieves exactly one rotation for each orbit.

But the second part is not exact. Because the orbit of the Moon is not perfectly circular its velocity is not constant: when getting closer to the Earth it accelerates ; and when getting further away, it decelerates (basically, the Moon is trading potential energy, or altitude ; with kinetic energy, or speed). With our modern knowledge, we know the velocity of the Moon changes between 962 m/s and 1096 m/s.

With a constant rotation but different speed, the Moon seems to be oscillating. It shows more than exactly half of it surface: smart people this phenomenon libration.

So, what?

Well, if the Moon is traveling at the correct speed such that its rotation and orbital velocity cancels, nothing happens. But if the orbital velocity is higher or lower, it will not show exactly the same face, and all our computations will be wrong.

Counting pixels, again

Let’s try again. Our previous equation is still correct, but Moon_diff_pxl needs some adjustments.

We will now call it diff_tot_pxl, and it is actually the sum of 3 numbers:

So we are missing Moon_orbit_pxl. We could compute it with two pictures, taken 24 hours apart: the position of the camera on the Earth would be the same, so Moon_diff_pxl would be zero. We could therefore measure Moon_rot_pxl + Moon_orbit_pxl by counting pixels just like we did.

Conclusion

Sadly Pauline did not take that third picture. That is why we can not finish our challenge, how sad!

Yes, the conclusion is short, it took me way to long to write this article and don’t want to delay it even more!